... more correctly speaking you see an “euclidean ab initio path integral tunneling trajectory corresponding to intramolecular intermediate-barrier proton transfer in malonaldehyde at room temperature in the gas phase”. The red balls symbolize oxygens, the grey balls are carbons, the white balls mark hydrogens, and the yellow hydrogen is the special one that forms a hydrogen bond between the two oxygens.

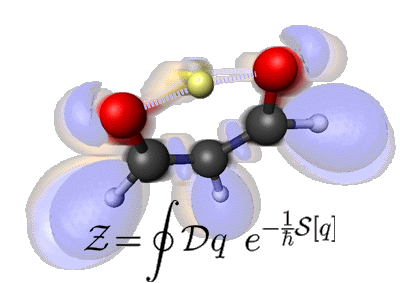
Note that this is not an artificial animation. Rather, the many-body interactions driving the motion you see are computed from ab initio theory. The transparent clouds superimposed upon the nuclear skeleton actually show how the topology of the electronic structure changes during this chemical reaction as probed by the so-called electron localization function ELF.

The resulting effective potential felt by the yellow proton corresponds roughly to a double-well potential: the two degenerate states of the system are “proton in the left well” (tan clouds) and “proton in the right well” (pink clouds). The two blue frames highlight the electronic structure at the transition state when the proton is midway between the two wells, deep in the classically forbidden barrier region. In the language of instanton theory, these frames correspond to the kink and antikink pair. The small excursions of all other atoms are essentially due to zero-point motion. Chemically speaking, these are the vibrations of the molecular frame, or the small-amplitude fluctuations that renormalize the minimum action path in the instanton picture. Finally, in the language of lattice field theory or quantum Monte Carlo, this periodic movie shows a typical word-line dynamically in euclidean time, which, was actually sampled by an appropriate molecular dynamics method. The depicted formula is the Wick-rotated Feynman path integral on which everything is based.